「音」の仕組みを理解する
音楽に限らず、生活する上で「音」は重要なものですが、この「音」とは一体どういうものなのでしょうか。
音とは空気の振動である、とは学校でも習う一般常識ですが、もう少し詳しく見てみましょう。
空気の振動は「振動」であり、「流れ」ではありません。
音の鳴るスピーカーの前に立っても風は感じませんが、空気の振動である音は感じることができます。
逆に外で風に当たっても、音は感じませんが空気の流れは感じることができます。
強い風はビュービューと音が鳴りますが、あれは空気の流れが物に当たるなどして振動を発生させているに過ぎません。
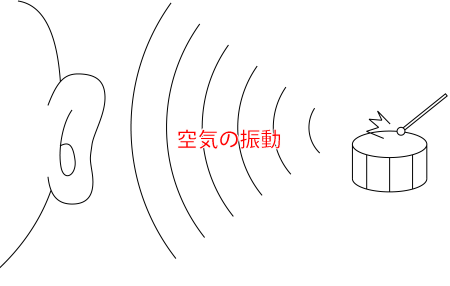
空気が振動し、その振動が耳の中の鼓膜に振動を伝え、音として聞くことができます。
振動とは「揺れ」のことで、一定の範囲を行ったり来たりすることです。
振動は風のように空気が一方から一方へ流れるのではなく、空気が一定の場所で行ったり来たりしている状態を人が感知する事で音として認識できます。
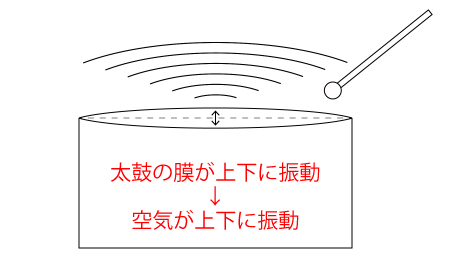
例えば太鼓を叩いた時、太鼓の膜が上下に振動します。
これは打撃により膜が一時的に引き延ばされ、伸縮により戻ろうとする事で発生する振動です。
膜が上に膨らむと、膜の周囲の空気が押され、気圧がわずかに上昇します。
部分的に気圧が上がると、それを解消するためにさらに周囲の空気も押され、同様の現象が遠くに伝播していきます。
反対に膜がへこんだ状態になると周囲の気圧が下がり、周りの空気が引っ張られます。
時間にすれば一瞬ですが、この運動の繰り返しが空気の振動になります。
太鼓のようにわかりやすい振動媒体がなくても、肉眼では見えない振動が発生しています。
ドアを叩けばドアが、地面を踏みつければ地面が振動して空気を振動させています。
(叩くのに使った物質も振動しています)
空気の振動は目で見ることはできませんが、これを視覚的に表示できるようにする機械がオシロスコープです。
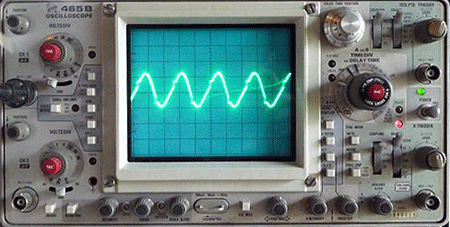
オシロスコープは空気の振動を電気信号に変換し、その電気信号を画面に表示します。
画面上に表れる電気信号の形を波形と言います。
波形編集ソフトやDAWでも波形を見る事が出来ます。
DAW上のオーディオトラックに表示される波形を拡大表示すればオシロスコープのように波の形を見る事ができます。
音の三大要素
音は、 高さ、音色、大きさの重要な3つの要素を持ちます。
音の高さ
ピアノなどの楽器や人の声などにも「高さ」「低さ」が感じられます。
これは空気が振動する速さを人が聞き分けています。
振動の速さを波形で表すとこのようになります。
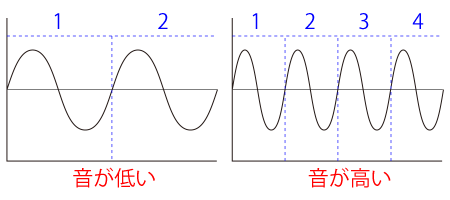
振動とは行ったり来たりすることですから、一往復して一回の振動となります。
波形で言えば真ん中を基準として上下を一回往復して一回の振動です。
1秒間に一回振動することを1Hz(ヘルツ)と言います。
ちなみに人が音として感じられるのはおおむね20Hz~20000Hzの間と言われていて、それを越える周波数の音は人には聞こえない超音波と呼ばれます。
(年齢を重ねると次第に高い音が聞こえにくくなってきます)
1000Hzは1kHz(キロヘルツ)と表すこともでき、20000Hzは20kHzと表せます。
上図では、同じ時間で左は2回の振動に対して、右は4回振動しています。
この時、左波形よりも右波形の方が音が高く聞こえます。
この振動の回数が倍になると、音程は1オクターブ高くなります。
左波形よりも右波形のほうが1オクターブ高い音が鳴っている、ということになります。
音色
ピアノ、ギター、フルートなどはそれぞれで音色が異なります。
音色の違いは波形では形に表れます。
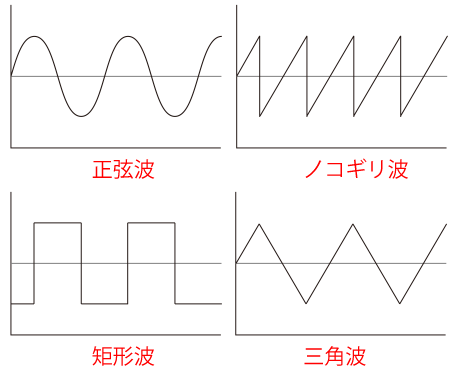
上図はアナログシンセの基本波形としてよく使われる波形です。
サイン波(正弦波)は倍音成分を全く含まない、滑らかで丸い音です。
ノコギリ波はすべての(整数倍の)倍音成分を含む、鋭い音です。
矩形波は奇数倍音のみを含む、硬い音です。
三角波は奇数倍音のみを含む、サイン波に似た柔らかい音です。
矩形波と三角波では奇数倍音の音量が異なります。
音は基音と倍音に分けることが出来ます。
基音は音程を決定し、倍音は音色を決定します。
サイン波以外の音には必ず倍音が含まれていて、この倍音がどのように含まれているのかによって音色が決定されます。
倍音はその名の通り、基音の周波数の整数倍の周波数です。
基音が100Hzならその倍音は200Hz、300Hz、400Hz…という風になります。
このときの100Hzの音を第1倍音(=基音)、200Hzを第2倍音…と言います。
倍音は第1倍音、第2倍音…と数字が増えるほど音量は小さくなっていきます。
たとえばノコギリ波では第2倍音は基音の半分の音量、第3倍音は1/3、第4倍音は1/4…となります。
矩形波では第2倍音、第4倍音、第8倍音…は全く含まないという特徴があります。
言いかえれば偶数倍の倍音の音量はゼロで、奇数倍の倍音のみを含むということです。
このような倍音成分の違いが音色の違いとして表れます。
整数倍以外にも倍音成分は存在しますが、非整数倍の倍音成分を多く含む音色からは音程感を感じられません。
こういった音色はクラッシュシンバルなどの音程を感じられない打楽器に多いです。
ただし「ドレミで表せない」というだけで、打楽器にも音の高い低いはあり、たとえばシンバルなら口径が小さいほど高い音が鳴ります。
音の大きさ
3つ目は大きさです。
波形上は上下の振り幅の大小が音量の大小になります。
音自体の音量の大小はそれほど重要な意味を持ちません。
音が大きくても小さくてもピアノはピアノで、聴きやすさや他の楽器とのバランスには関係しますが音そのものの要素ではありません。
重要なのは時間による音量の変化です。
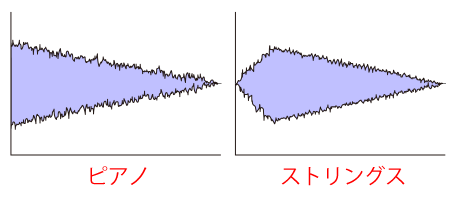
例えばピアノの音は、鍵盤を押した瞬間に最大の音量で発音され、音量は次第に減衰していきます。
ストリングスのような楽器の音の立ち上がりは比較的ゆったりとしています。
(ただし実際の時間にすればコンマ数秒のわずかな時間です)
このような時間的な音量変化がそれぞれの楽器の楽器らしさと言えます。
仮に波形編集でオルガンのように音が減衰しないピアノを作っても、それをピアノの音と認識することは難しいでしょう。
ピアノのアタック部分(発音の一番最初の部分)の音量をゼロにしてしまうとこれまたピアノの音と認識することは難しくなります。
■ピアノのエンベロープの例
前半は素のピアノの音、後半はアタック部分を削ったピアノの音です。
これら3つの要素によって音が決定されます。
アナログシンセではこういった要素を調整することで音作りをしていきます。
ついでに、波形の合成について説明します。
2つの波形を単純に混ぜ合わせた場合、以下のように合成されます。
波形の合成は単純に足し算した音が出力されます。
例えばある時点の音量を数値化した時、一方が5でもう一方が3なら合計は8となり、音量が大きくなります。
両方が同じ方向に振れているならば音量は単純に大きくなります。
一方が5でもう一方が-3なら合計は2となり、音量は小さくなります。
一方が2でもう一方が-8なら合計は-6となり、音量は大きくなります。
(加算される波形側から見れば音量は小さくなる)
波形はマイナス方向に振れることになります。
音量はゼロから離れるほどに(波形の振り幅が大きくなるほどに)大きくなることに注意してください。
マイナス方向だから音量が小さいということではありません。
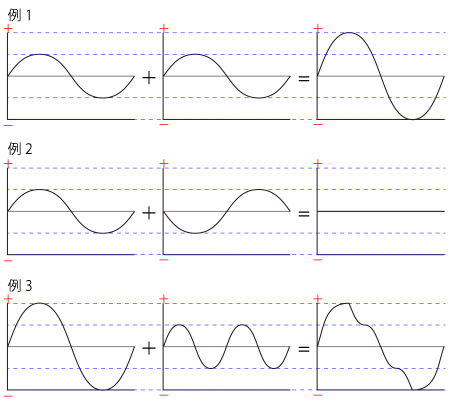
例1は同じ波形を重ねた場合で、単純に音量が2倍になります。
例2は上下が逆になった波形同士を重ねた場合です。
一方がプラス側に振れるに従って、もう一方が同じ割合でマイナス側に触れるので、足し算の結果出力される音量は常にゼロとなります。
このような上下が反転した波形を逆位相、位相の反転といいます。
ある波形に逆位相の波形を合成すると無音になるということは知っておいてください。
例3は1オクターブ高い音を半分の音量で重ねた場合です。
出力波形はややいびつな形になりますが、これは第1倍音の合成と同じ事をしています。
さらに1オクターブ高い音(第3倍音)を半分の音量で、さらに1オクターブ高い音(第4倍音)をまたまた半分の音量で…と何回も重ねていくと最終的にノコギリ波の形と同じになります。
実際にはもっと複雑な波形同士を混ぜ合わせるので図で表すことは困難になります。
アナログシンセではこれを意識して音作りをすることはあまりないかもしれませんが、頭に入れておいてください。